从零开始学习PYTHON3讲义(二)
把Python当做计算器

《从零开始PYTHON3》第二讲
上一讲我们说过了如何启动Python IDLE集成开发学习环境,macOS/Linux都可以在命令行执行idle3。Windows则从开始菜单中去寻找IDLE程序的图标。
 上一讲我们还见到了Python的两种工作模式,交互模式和程序模式。
上一讲我们还见到了Python的两种工作模式,交互模式和程序模式。
通常在一个大型的系统中,程序模式是必然的选择。因为一个完整的项目,都需要大量的准备工作。为很多运算的必要条件准备最初的值(专有名词也叫“初始化”),接下来的运算也往往逻辑复杂,需要作出多种选择和频繁的组合计算。这个过程,需要用计算机能明白的文字完整描述出来。描述的过程,也就是称为编写程序的过程。(下图仅为示意性,先不要管程序的内容)
 命令行方式则看上去更简单,Python对你的每条命令即时的给出反馈,适合用户边想边试,快速的看到结果,并根据结果调整策略、再次尝试。
命令行方式则看上去更简单,Python对你的每条命令即时的给出反馈,适合用户边想边试,快速的看到结果,并根据结果调整策略、再次尝试。
Python语言应用于工程界和科学界的时候,经常就是工作在这种模式。交互模式下一遍遍尝试的过程,实际也是“研究”的过程。当然研究取得了成果,最终还是需要用“编程”的模式,把研究结果变成一个产品。
通常这样编写的程序的主体部分,就是在交互模式中,顺序输入的命令的总和。
在我们刚刚接触Python的阶段,交互模式也为我们的学习提供了良好的支持,动手实验每一个小的学习过程,根据反馈的结果验证我们的思考。学习->思考->动手验证->再次学习,这是我们学习的一般路径。
 启动IDLE程序之后,Python默认就工作在交互方式下,也就是上面这张图的样子。在File(文件)菜单中选择New File(新文件)或者Open(打开)以前的老程序,则Python会再打开一个窗口,在新窗口中可以编辑、修改程序,也就是程序模式。本节课我们主要讲解交互模式。
启动IDLE程序之后,Python默认就工作在交互方式下,也就是上面这张图的样子。在File(文件)菜单中选择New File(新文件)或者Open(打开)以前的老程序,则Python会再打开一个窗口,在新窗口中可以编辑、修改程序,也就是程序模式。本节课我们主要讲解交互模式。
交互模式可以完成很多工作,在其它编程语言中需要用复杂的程序才能完成的工作,可能在Python交互模式中简单的几条命令就能完成。今天实际是我们正式踏上编程之旅的第一课,我们从最强大易用的Python数学计算来开始。
把Python当做计算器
首先是最基本的四则运算和常用的乘方:
| 数学运算 | 操作符 |
|---|---|
| 加法 | + |
| 减法 | - |
| 乘法 | * (不是✖️) |
| 除法 | / (不是➗) |
| 乘方 | ** |
这是最好理解的部分,加、减两项运算跟我们数学课上学的完全相同,乘法、除法、乘方的运算符则使用了替代的符号。
这样设计的原因说起来话题比较长。
大概讲就是计算机发展之初,输入设备是由传统的英文打字机改装而来的,键盘布局当然就采用了同英文打字机相同的布局。
但是在这种布局上,加、减符号是有的,乘除符号则没有,因此乘法使用了从外形看比较接近的“*”,除法则使用了意义上最接近的“/”。
为什么不使用“x”?当然是为了避免歧义。
下面就是几个简单四则运算的例子,希望你也多动手试试:
>>> 2 + 2
4
>>> 50 - 5*6
20
>>> (50 - 5*6) / 4
5.0
>>> 8 / 5
1.6
>>>5**2
25
>>>2**7
128
上面这种代码块,在我们以后的讲解中还会不断的出现,所以我们这里给出一个简单的说明。
通常程序的讲解,最重要的是能容易的定位到某个特定位置。定位的方法最直接就是使用第几行、第几列这样的方式,因此代码块要能清晰的体现出来行、列的关系。行的位置在代码块中使用了行号,就是你在这个例子中看到的从1到12的编号,比如说第4行的数字20,就是第三行命令的执行结果,这看起来非常清楚。
列编号显然不那么方便,但程序字体都会额外要求“相等宽度”,这样你偶尔需要去计数和分辨格式的时候,就容易了很多。
程序块通常还使用颜色“区分”程序不同部分的要求,上面的例子能看到颜色的变化,但是还不够明显,我们在以后的讲解中你会看到更清晰的例子。
言归正传我们再说一下跟交互方式相关的内容:
>>>符号,也就是3个大于号,这个是Python交互模式的“提示符”,意思是说“Hi,我准备好了,你可以输入命令了!”。
见到这样的提示符,在其后输入你的命令,才能被Python交互方式所接受。再说一遍,这是Python交互模式在做完上一个任务、并且完成自身准备之后,主动给出的,不是你输入的,你输入的话,因为并没有一个命令是3个大于号,所以也无法被Python交互模式所识别,只会给出报错信息。
在提示符之后,你输入的每条命令,最后都要使用“回车键”来告诉Python:“我的命令输入完了,你开始执行吧!”。在我们使用的电脑上,回车键通常标记为“ENTER”或者“RETURN”,不同的键盘可能有不同的标注,现在电脑和手机这么普及了,我相信你早就知道了。
回车符在屏幕上并不会特别的显示出来,你唯一能看到的就是引导文字输入位置的光标,换了一行并出现在行的最开始位置,所以回车符也称为换行符。随后很快的等Python处理完命令,在这一行开始的位置开始显示命令计算的结果。从上面的代码块例子来看,偶数行,都是Python计算上一条命令所输出的结果。结果显示完成后,Python再次给出“»>”提示符,等待你的下一条命令。
刚才我们讲过了,交互模式每输入一条命令,Python都会立即执行,并给出结果反馈,这会让我们产生一种误解,似乎Python反馈的结果,就是由上面输入的这一条命令决定的。事实并非如此,Python每一次的反馈,都是由Python启动之后,输入的所有的命令累计一起,互相作用,所得到的结果。你之所以有误会,是因为你输入的命令,可能之间并没有什么相互影响的关系,所以这种“累计”没有体现出来而已。之所以每个程序都需要由大量的命令组合而成,就是因为这种“累计相互作用”的结果。这个我们在后面会详细讲。
请尽量的多动手做一些练习来尝试使用Python进行四则运算。对于本课程的学习者来说,四则运算太简单了,但是希望你能从开始学习编程的心态来看待这些练习。所有的学习,都是从你已知的知识开始,接触新知识,从而探索你所不知道的部分。如果上来就用你不懂的概念来解释另外一个你不懂的概念,你一定会崩溃。
练习中还有一个对于亚洲人非常重要的注意事项:计算机在西方发明之初,实际上只有英文的处理能力。直到上世纪80年代,才有了中文的输入法和电脑上的中文字符。所以,所有在Python(以及几乎所有的主流编程语言中)使用的命令,都只能接受英文的字符输入,中文字符、其它国家的语言字符,可以被Python处理,但并不能当做命令。
这些中文的字符,通常比同样的英文字符要宽一倍,被称为“全角”字符,对应的英文字符就是“半角”字符。最可怕的还有比空格字符宽一倍的中文空格。这种出现的错误非常难以排查。所以如果看起来没有敲错,但Python持续报错,建议你仔细用英文半角字符重新输入。使用英文半角字符,其实就是关闭中文输入法的情况下输入的字符。下面的程序块示意性的让你看到这种区别:
+ #奇数行:英文半角字符
+ #偶数行:中文全角字符
-
-
*
*
/
/
回到使用Python做数学计算。在复杂计算中,运算优先级是必须考虑的问题,上面的例子你已经看到了使用括号( )来确保优先执行的例子。Python的运算优先级跟数学中的定义是相同的:
| 数学运算 ,优先级由高到低 | 操作符 |
|---|---|
| 括号 | () |
| 乘法、除法 | * / |
| 加法、减法 | + - |
在Python和大多的编程语言中,大括号{}、中括号[]都是有特定作用的,不能当做Python中的数学符号来使用。在数学中多重括号需要用到大括号和中括号的地方,可以重叠使用小括号()来实现,这种多重的重叠使用在编程中也称为“嵌套”。
>>> (5+((3+2)*7-227))/4
-47
练习时间
1.请使用Python的交互模式来计算下面算式的值:
2100-21×53+2255
(103-336÷21)×15
800-(2000-9600÷8)
40×48-(1472+328)÷5
(488+344)÷(202-194)
2940÷28+136×7
2.如何求开平方运算?
应用题
每个程序编写之前,都要先弄明白这个程序是干什么用的,运行在什么样的情形之下,解决什么问题。这些前置的条件,有一个专有的名词叫“程序需求”,也就是说,编程序的第一步是弄清楚“需求”。
这很类似上面的这些数学算式,每个枯燥的算式背后都有其背景,这个背景就是应用场景。下面我们就看一个应用题的例子:
某班有50名学生,准备集体去看电影,买到的电影票中,有30元一张的,有20元一张的。已知买电影票总共花1240元,问票价是30元和20元的电影票各几张?
现在回答小学的问题,肯定容易的很。 设票价是20元的电影票为X张,则票价为30元的应有(50-X)张。 可列出方程:20X + 30(50 – X)= 1240 化简方程:X=(30x50-1240)➗(30-20),随后就可以在Python中计算了。
>>> (30*50-1240)/(30-20)
26.0
求得X=26之后,50-X,可以得到票价为1.5元的电影票张数:24。我们在Python中计算的时候,可以直接使用:
>>> 50-26
24
还可以在X计算结束之后,直接使用:
>>> (30*50-1240)/(30-20)
26.0
>>> 50-_
24.0
这个“_”,就是减号“-”键按住SHIFT键才能打出来的第二功能键。在Python交互模式中,“_”保存了上一次计算的结果,等于把上一次的计算结果,替换到“_”出现的位置。
所以“_”符号,必须在所需要的计算完成之后,马上使用才有效。如果还进行了其它计算,那“_”的值,会变成新计算的结果值。
这种功能是计算机的记忆保存功能,“_”也被称为“结果变量”。
变量
变量这个词也源于数学,是计算机区别于其它非智能计算设备很重要的一个体现。变量的概念是所有编程语言中的重点之一。
你可以把每个变量理解为一个空盒子,盒子中可以用来保存物品,当然这里就是数据。每个盒子都要有一个容易记忆的名字,好让你在需要的时候使用特定的盒子。盒子能够在需要保存的时候放入数据,在需要用到的时候再取出数据。为了保存新的数据而不影响原来保存过数据的盒子,我们可能需要建立一个新的空盒子来保存新的数据。总结一下刚才说到的这几种操作,我们可以得到变量的几个要素:

- 变量名;
- 变量的值;
- 变量的声明(准备新的空盒子);
- 变量的初始化(把值保存到盒子);
几乎在所有的编程语言中,学到变量,都要关注这几点。 在Python中,因为变量并不需要声明,每当你第一次使用一个变量名的时候,Python会自动的完成“新盒子的准备工作”,所以通常在Python中,你只要关注1、2、4共3点就好。
变量值的概念,是相对“立即数”常量而言的,上图盒子中的数字“2”,上一节中我们使用Python计算器时候输入的那些数字,都是常数。在电脑中因为是无需计算就能知道的值,所以也叫“立即数”。一个立即数总是显而易见确定的,不会变化,因此在这里也可以称为常量。
立即数是确定的值,不可能变化。而变量,就是一个盒子,其中的容纳的数字,当然可以变化。
这个变化是指变量盒子可以保存不同的值。而在一个特定时刻,变量的值当然是确定的。
不要把变量跟数学中的未知数弄混,变量的值在任何一个特定时刻都是确定的,在Python中使用的时候,就当做那个确定的值来使用,是不折不扣的已知数。容易混淆的原因不过是因为变量名看上去像数学中的未知数而已。比如变量名和未知数可能都刚巧叫做“X”。
每种编程语言对于变量的命名都有一定规则,这是语言语法的一部分。Python对变量名的要求非常简单:以任何字母开头,后面可以是数字或者下划线“_”。 Python3中还允许使用中文作为变量名,但是因为兼容性、效率、容易出错等原因,我们不推荐大家使用中文变量名。
语法之外,通常还有非强制性的习惯来规范变量名的写法,比如:尽量使用有意义的单词或者拼音来当做变量名。多个单词的变量名,每个单词的首字母大写或者在两个单词之间使用下划线。比如下面就是几个有意义的变量名:
dogs rabbit1 price jia_ge numberOfBalls
下面几个则算是不太理想的变量名:
abc aaa xyz
再下面几个,干脆是非法的变量名,用在Python中会报错:
2floor balls!
numberOfBalls这样的命名规则俗称叫做“驼峰命名法”,原因你懂的。 jia_ge这样的方式则称为:“下划线命名法”
变量就像一个空盒子,只有其中保存了值,变量才有意义。让变量保存确定值的过程就是为变量“赋值”。变量声明之后的第一次为变量赋值的操作被称为“初始化”。当然因为Python不需要变量声明,所以初始化跟赋值,在Python语言中看起来没有什么不同。
比如我们为两个变量赋值:
x = 42
y = 42
用图来表示的话,大概就是这个样子:
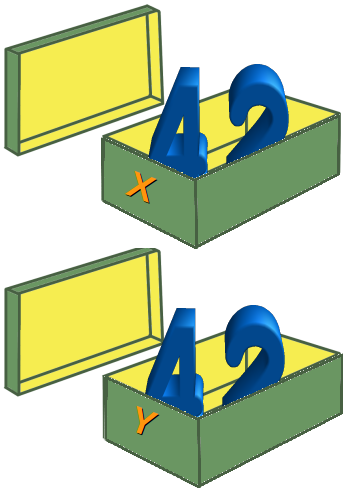
这里特别要注意的,是Python语言中的等号“=”是赋值命令的意思,或者叫赋值运算符。表示把“=”右侧的值,赋值给“=”左侧的变量。这跟数学中学到的等式是完全不同的概念。几个重点:
- “=”左侧必须是可以用来保存值的变量名,也称为“左值”。
- “=”右侧必须是类似“42”这样的立即数,或者是合法的表达式可以计算出数值,也称为“右值”。
- “=”左右侧的内容含义是确定的,不是等式,不可以左右侧内容互换。
修改变量的值就是为变量再次赋值,跟初次为变量赋值没有什么不同。
下面我们使用变量的方法,再来计算一次上面的应用题:
某班有50名学生,准备集体去看电影,买到的电影票中,有30元一张的,有20元一张的。已知买电影票总共花1240元,问票价是30元和20元的电影票各几张?
- 设票价是20元的电影票为X张,则票价为30元的应有(50-X)张。
- 可列出方程:20X + 30(50 – X)= 1240
- 化简方程:X=(30x50-1240)➗(30-20),Y=(50-X)。
在Python中计算一下试试吧。
说了变量,我们对应说了立即数。其实在其它语言中还有常量的概念,顾名思义,在程序完整的运行过程中,不能被修改的量就是常量。在Python中没有常量的概念。但我们在学习中,思想上还是要有常量的概念,因为毕竟有很多值是常量,比如π,比如常数e,比如重力加速度g。
前面讲过,立即数也是常量的一种,称为常数。
函数
今天我们的概念都是围绕着初级的数学概念展开的。当然也不能少了函数。有个很形象的图可以描述函数的功能:
有特定的输入,经过一系列的计算,完成特定的输出,这就是函数的功能。数学中的y=f(x),x是输入值,y是输出值(数学中是等式,所以称为y是输出值,在Python中的话,y是保存了输出结果),f()就是函数本身。
函数的详细内容我们会在下面一讲进行,这里只介绍一个非常常用的Python内置函数print(),功能是输出参数的值。
比如上面一节的练习,如果你真的做了的话,会发现计算X和Y的值,似乎都没有得到期望的结果。原因是计算的结果被赋值给了变量X或者Y,因此没有自动显示到Python交互式环境中,因此你没有办法像前面的那些计算一样,直接看到结果。如果想看到结果怎么办呢?就是使用print()函数:
>>> print(X,Y)
(26.0, 24.0)
在一个大的程序中,通常都要把程序按照功能划分,使用很多个小的函数来实现,并组装到一起。因此函数通常也被称为子程序,但严格意义上讲,通常只有没有输入值、输出值的函数才可以称为子程序。
整数和小数
几乎所有的计算机都非常擅长整数运算,而通常整数运算也非常适合某些场景。比如屏幕分辨率是1920*1080,在绘图中计算出来小数通常也没有意义;玩游戏,打出了5发炮弹,计算出来5.5发也同样用途不大。
整数的运算在计算机中如此重要,以至于虽然同样是数学运算,整数运算和带有小数的运算被大多数编程语言当做两种类型来区别对待。这样在特定的运算场景中,速度更快,精度更高。
整数的例子:3 4 5 101 256
小数的例子:3.14 1.414 2.1343e02
在计算机表示小数的时候,通常使用科学计数法,小数点的位置在科学计数法中是固定的,但跟原值比都不是原来的位置,因此也被称为浮点数。以后我们都用“浮点数”这种更准确的方法来称呼小数。
在实际应用中,经常会发生两种类型的数据互相转换的情况,你会频繁的看到。
整数可以直接当做浮点数来使用,不需要转换,但是要求算式中,有浮点数先参与了运算,比如5.1+4,4虽然是整数,但因为5.1是浮点数,整体算式会自动采用浮点数的方式来计算。整数常数转换成浮点数,可以在其后加上小数位,比如:4.0。
浮点数转换成整数则需要明确的指定转换,这也称为“显式”的转换。
-
使用int()函数转换,比如int(3.54)的结果是3,小数部分,无论多少,都会舍去。
-
如果希望四舍五入,要附加使用round()函数,比如int(round(3.54)),结果是4。round()函数的功能是四舍五入,但结果依然是浮点数,上例中是4.0,所以还要再经过一次int()函数转换。
针对整数和浮点数两种不同的类型,运算也有一些区分:
| 整数运算 | 浮点数运算 |
|---|---|
| 除法: 17 // 3 取余数:17 % 3 |
除法:17 / 3 没有取余数的运算 |
| 赋值: a = 5 | 赋值:a = 5.0 |
整数运算和浮点数运算,虽然都是数学运算,也没有数学意义上的难度,但是很重要,我们后面的课程会有大量不同类型的运算,所以一定要理解清楚两者的区别。浮点数、整数转换、整数运算相关的内容,暂且先以了解为主,后面我们还会详细讲解。
练习时间
使用Python计算下面应用题:
甲、乙两人相距36千米,相向而行,如果甲比乙先走2小时,那么他们在乙出发2.5小时后相遇;如果乙比甲先走2小时,那么他们在甲出发3小时后相遇,甲、乙两人每小时各走多少千米?(假设甲乙的速度均匀稳定)
本课程结尾的练习,通常是要求在辅导老师的帮助下由学生自己完成。并且课程所留下的练习时间一般无法让学生能够完成所有练习,所以需要学生回家后继续,直至完成所有练习项目。
本讲小结
今天是大家开始Python编程学习的第一节,介绍了Python的两种工作模式,交互式模式和程序模式。并且使用交互模式的计算器功能让大家使用小学数学的知识,开始熟悉Python的使用。
先学习了Python的基本运算和运算优先级。然后学习了变量、函数的基本相关知识。理解变量的概念是学习的重点。
我们还穿插介绍了全角、半角的区别,这是初学中容易犯的错误,需要特别注意。
本讲的练习重点是用Python语言的方式,来描述通常所见的数学公式,从而使用Python完成数学计算。在这个过程中,解题思路、题目含义等都属于数学范畴,并不在本课的讨论范围内,我们尽力使用非常简单的数学概念来引导大家入门Python的学习。
部分练习答案
1.开平方,也就是求平方根,可以使用指数的倒数形式,比如:
>>> 3 ** 0.5
1.7320508075688772
>>> 3 ** (1/2)
1
>>> 3 ** (1.0/2)
1.7320508075688772
注意上面第3行,因为1、2都是整数,所以实际当做了整数除法,而结果是0,所以导致3 ** 0结果是1。这种情况下应当采用第5行的形式,强制要求浮点运算。
2.最后应用题的思路
- 假设甲的速度为x千米/小时,假设乙的速度为y千米/小时
- 列方程式(2.5+2)x+2.5y=36,3x+(3+2)y=36
- 根据方程2推导为:x=(36-5y)/3,代入方程1
- y=(54-36)/5
- 最后得:y=3.6,将y值代回方程,得到x=6
有些同学可能希望更多的了解数学计算的知识,今天课程中的数学内容显然太简单。
Python官方提供了数学计算库math,有能力的同学可以参考官方的文档:https://docs.python.org/3/library/math.html,我们以后的课程也会按照计划做摘要的介绍。
