从锅炉工到AI专家(5)

图像识别基本原理

从上一篇开始，我们终于进入到了TensorFlow机器学习的世界。采用第一个分类算法进行手写数字识别得到了一个91%左右的识别率结果，进展可喜，但成绩尚不能令人满意。
结果不满意的原因，当然还是算法太简单了。尽管我们都已经接受了“所有问题都可以用数学公式来描述”这个观点，但直接把一幅图片展开的784个数字作为方程式参数进行一个线性运算+非线性分类器就叫做“人工智能”怎么都感觉那么不靠谱…至于能得到91%不高的识别率，从这个意义上说，似乎都令人有点不太相信。这个不相信不是指91%太低了，而是这种玩笑一般的计算就有91%的准确率有点奇幻啊。
其实数学的魅力就是这样，看起来公式简单，但上一节就说了，你别忘了是784维啊，手工计算肯定会疯掉的。
如果利用上一篇介绍的小程序，把我们图像识别程序学习过程完成后所计算的权重矩阵W的10个维度都转换成28x28分辨率的图片（还记得吧，我们的权重矩阵W是784x10,其中784就是28x28得来的)，然后做一些着色渲染，看到的会是这个样子：

其中红色的部分代表权重是负值，蓝色的部分代表权重是正值。
以字符0为例，图中红色的部分代表，如果要识别的图片，上面这个位置有手写痕迹的话，那这幅图片更趋向于不太可能是字符0。而蓝色的部分，则代表如果同样位置有手写痕迹的话，那图片更趋向于可能是字符0。这样全部28x28=784个数据都用这种方式计算，最后的结果，当然就代表更接近字符0的可能性。这就是这个程序图像识别的基本原理。
我们在这里把这个权重图给出来的原因，就是虽然这个算法简单，但能更清晰的表现“机器学习”的数学含义。接下来的“神经网络算法”及其它算法，因为复杂度高，单纯结果的权重往往已经不能用这种直观的方式表达出来了。

神经网络

在官方MNIST的案例中，神经网络的部分是直接跳过了的。因为随着技术的发展，在图像识别这个问题上已经有了更好的算法，就是“卷积神经网络”，这个实现我们下一篇再讲。
实际上我觉得，“神经网络”这个概念无论如何是跨不过去的，不然后期的很多概念都无法讲下去或者讲了也无法让人理解。科学总是这样，大多时候即便没有巅峰突破，普通的工作也并非可以省略，不然就成为了空中楼阁。
“神经网络”的诞生是自然选择的结果，人脑就是由无数个神经元组成的，有资料说大概接近900亿个，是天文数字的级别。这些神经网络的传导和反射支撑着现代人类所有的智力和行为。

在人工智能还没有足够现代理论支撑的年代，仿照人脑“神经网络”的工作模式，建立“人工神经网络”进行机器学习是很自然的事情。并且在实践中的结果也非常令人兴奋，所以从并不很长的AI历史上，“人工神经网络”算统治了相当不短的时间。以至于对于很多非专业人士来讲，“神经网络”已经成了AI标志性的概念。

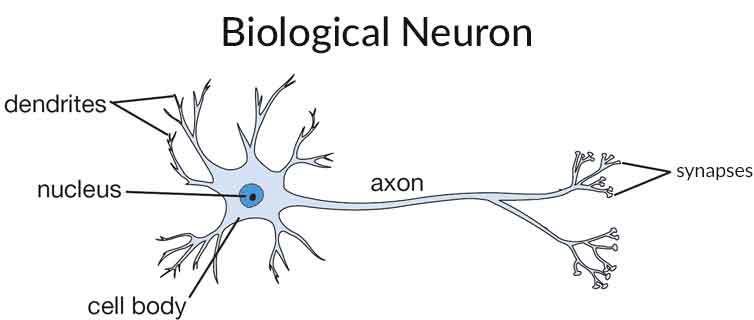
模仿人脑神经元细胞的基本工作方式，下图示意了一个“人工神经网络”基本单元的工作方式：

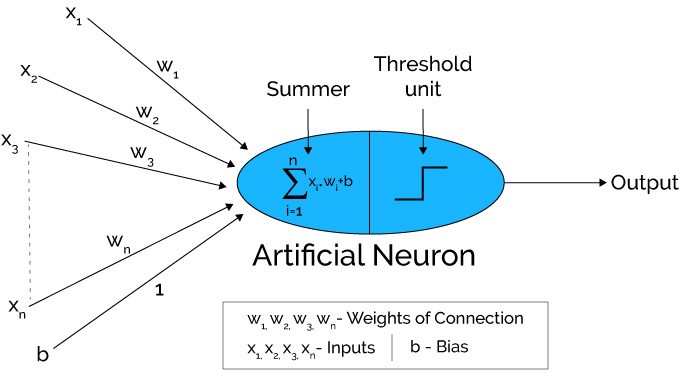
每一个这样的计算节点，都有n维的输入，在其中完成一个类似上一个源码样例中的线性计算，然后汇总输出，这个输出会再连接到下一级的计算节点。很多个这样的计算节点汇总完成一组计算，这样成为一“层”。上一层的输出，成为下一层的输入，多个层次累计起来，完成最终的机器学习过程。 在这些多层的计算中，第一层承担了所有原始数据的输入，因此叫做“输入层”；最后一层完成结果的输出，叫做“输出层”；中间的部分承担上一层的结果，经过计算完成下一层的输入，但对用户来讲实际是不可见的，叫做“隐藏层”。这几个概念以后你在看各种资料的时候会经常看到，你需要知道这些概念指的是什么。

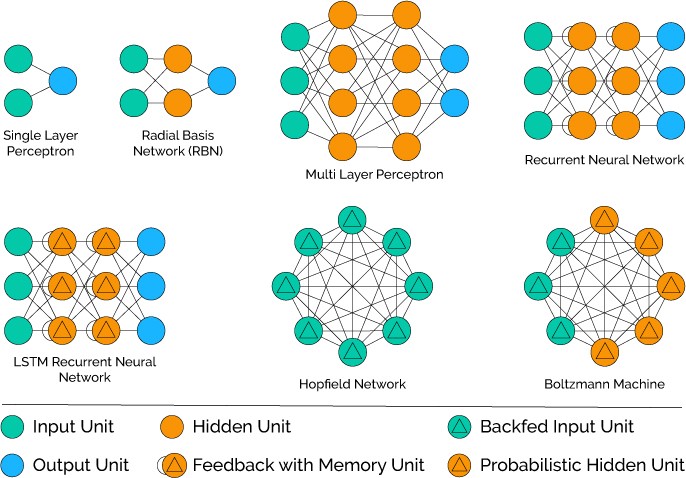
上图示意了神经网络的多种变形和组合后的网络模式。这种“仿生学”一般的组合模式取得了令人惊喜的效果。从数学的计算结构上非常的清晰，但内部多节点组合之后的数学机理实际上至今也没有哪篇论文描述的非常清楚。你可以理解为：通过增加计算节点、更多的体现和保持每个数据和其它数据之间的微小关系甚至多层互动之后的关系，从而更准确的完成对结果的计算。

反向传播

有了已经内置的神经网络算法实现之后，普通用户对于算法的内部数学实现肯定关心的更少了，这里也只说一个重点。
线性回归方程中，我们使用梯度下降法解方程，每一次计算都可以通过代价函数的表现决定我们下一个计算的走向。
在多层神经网络中，这种解方程方式显然不灵了。因为最终的结果，跟最初的输入，中间隔了多个隐藏层。
因此“人工神经网络”的求解主要依赖“反向传播”的方式来进行求解，大意是指最后一层得出结果后，通过这一层的代价函数修正本层的权重W和偏移b，并把信号反向传递到上一层，从而让上一层也可以调整自己层的W/b,逐次反向传播，一直到输入层。

激活函数

前面一个独立神经节点的示意图中，你可能注意到了除了我们上一个例子中熟悉过的线性公式。
其后部还有一个“Threshold unit”,也就是“阈值单元”。在真实的世界中，我们的大脑不太可能对于任何需要处理的问题，都动用全部的大脑。
而根据上面那副“人工神经网络”示意图可以看出，所有的节点，虽然有层的划分，实际上是全连接的。
全连接的意思也就是对于任何一个输入，事实上所有的单元都会参与计算，这显然也是不合常理的。
那每个节点最后的阈值单元，就是用来决定对于某个任务，本节点是否参与以及以何种方法参与到最终的计算中。这个动作，在机器学习中也称为“激活函数”。
常用的激活函数有好多种，比如我们前面提过的sigmoid函数，上一次提到它是因为这个函数可以用于做0、1分类。这个函数的输入值如果小于0.5，则输出为0；输入大于0.5，则输入为1。
还有tanh激活函数，输入小于0则输出0，输入大于0，则输出1。
最后则是本次我们会采用的激活函数ReLu，它的输入如果小于0，则输出0，输入如果大于0，则原样输出。
这些数学特征，决定了所采用的神经元单元以何种方式参与到整体的计算。具体如何选择，依赖于我们要解决的问题。如果问题比较复杂，无法一下想清楚如何取舍怎么办？那，这么易用的工具和框架，这么小的代码量，都试一遍又何妨？

神经网络图像识别源码

#!/usr/bin/env python
# -*- coding=UTF-8 -*-

import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

import tensorflow as tf
sess = tf.InteractiveSession()

#对W/b做初始化有利于防止算法陷入局部最优解，
#文档上讲是为了打破对称性和防止0梯度及神经元节点恒为0等问题，数学原理是类似问题
#这两个初始化单独定义成子程序是因为多层神经网络会有多次调用
def weight_variable(shape):
    #填充“权重”矩阵，其中的元素符合截断正态分布
    #可以有参数mean表示指定均值及stddev指定标准差
  initial = tf.truncated_normal(shape, stddev=0.1)
  return tf.Variable(initial)
def bias_variable(shape):
    #用0.1常量填充“偏移量”矩阵
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)


#定义占位符，相当于tensorFlow的运行参数，
#x是输入的图片矩阵，y_是给定的标注标签，有标注一定是监督学习
x = tf.placeholder("float", shape=[None, 784])
y_ = tf.placeholder("float", shape=[None, 10])

#定义输入层神经网络，有784个节点，1024个输出，
#输出的数量是自己定义的，要跟第二层节点的数量吻合
W1 = weight_variable([784, 1024])
b1 = bias_variable([1024])
#使用relu算法的激活函数，后面的公式跟前一个例子相同
h1 = tf.nn.relu(tf.matmul(x, W1) + b1)

#定义第二层（隐藏层）网络，1024输入，512输出
W2 = weight_variable([1024, 512])
b2 = bias_variable([512])
h2 = tf.nn.relu(tf.matmul(h1, W2) + b2)

#定义第三层（输出层），512输入，10输出，10也是我们希望的分类数量
W3 = weight_variable([512, 10])
b3 = bias_variable([10])
#最后一层的输出同样用softmax分类（也算是激活函数吧）
y3=tf.nn.softmax(tf.matmul(h2, W3) + b3)

#交叉熵代价函数
cross_entropy = -tf.reduce_sum(y_*tf.log(y3))
#这里使用了更加复杂的ADAM优化器来做"梯度最速下降"，
#前一个例子中我们使用的是：GradientDescentOptimizer
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
#计算正确率以评估效果
correct_prediction = tf.equal(tf.argmax(y3,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
#tf初始化及所有变量初始化
sess.run(tf.global_variables_initializer())
#进行20000步的训练
for i in range(20000):
    #每批数据50组
  batch = mnist.train.next_batch(50)
  #每100步进行一次正确率计算并显示中间结果
  if i%100 == 0:
    train_accuracy = accuracy.eval(feed_dict={
        x:batch[0], y_: batch[1]})
    print "step %d, training accuracy %g"%(i, train_accuracy)
    #使用数据集进行训练
  train_step.run(feed_dict={x: batch[0], y_: batch[1]})

#完成模型训练给出最终的评估结果
print "test accuracy %g"%accuracy.eval(feed_dict={
    x: mnist.test.images, y_: mnist.test.labels})

这个程序中使用了3层的神经网络，经过20000*50个数据的训练，最终正确率可以达到96%以上，比上一个例子有了明显的进步。
实际上一个例子和本例，最终我们都使用的tf.nn.softmax()函数。看到其中的“nn”没有，这是“Neural Networks”的缩写，也就是说，不仅本例是神经网络算法，其实上一个例子，同样也使用了神经网络算法。
如果是以前没有TensorFlow的年代，这种特点我们能在算法源码中看的一清二楚，而现在，很容易就会忽略掉。
那么上一例中，我们实际上使用的是只有“一层”的神经网络算法，数学公式简化后，也就是普通的线性算法，然后经过非线性的softmax分类。
本例则毫无疑问是一个经典的神经网络算法，3层分别是784个输入->（输入层）1024个节点->（隐藏层）512节点->（输出层）10节点输出。
神经网络每一层之间是如何连接起来的呢？很简单，就如同程序中所示，每一层在公式那一行，其中计算时所引用的变量，是上一层输出的变量，就等于将各层进行了链接。TensorFlow会自动在这个计算图中上一层之后，添加上这一层的节点。
为了得到更好的识别结果，我们还采用了AdamOptimizer优化器进行“梯度最速下降”。TensorFlow中内置了好几种算法，数学实现可以参考最下面的参考链接。
那么神经网络的设计，究竟应当采用多少层网络？每层多少个节点？
这个目前没统一的标准，一般而言，层数越多、节点越多，就可以得到更好的识别率，但同时这个模型的工作速度也会越慢。还可能会有更大的“过拟合”风险。过拟合我们后面再介绍。
而且识别率的一点点增加，往往会需要更多的计算节点，成本不一定划算。
并不像增加一整层那样剧烈的资源消耗增加，在一个层中适当增加节点数通常是比较划算的方法，具体情况，也是要靠实验测试和科学评估的来决定。
多层的神经网络，因为网络深度的增加，也被称为“深度神经网络”(Deep Neural Networks / DNN)，这个简写经常会跟CNN(卷积神经网络)、RNN(循环神经网络)一起出现。

小说明

最近为了写这个系列，在网上翻找参考资料，另外也试图寻找一些现成的图片帮助概念的解释行文。结果在很多介绍机器学习的文章中，发现大量的谬误，读之冷汗不绝啊。
这也提醒我，一方面我尽力的校对并再次厘清概念，防止本文出现类似的低级错误。当然水平所限，难免仍然有一些错误无法发现或者认知本身就有误，欢迎各界高手指正也让我不断进步。
另外一方面总体感觉，可能是发展“大跃进”的原因，而且毕竟国内的基础水平进展偏慢、偏晚，很多译文及“教程”是概念错误的重灾区。
原本因为我主要面对身边及国内的读者，希望尽可能引用的参考资料都来自中文资料，但到了今天决定彻底放弃这个想法。能有质量相当的中文资料更好，如果没有，也只好引用一些国外的资料，毕竟不仅仅水平上，只说认真程度上就完全没法比。
我想这可能也是当前国内技术界普遍应当重视的问题。水平是一方面，态度则是更重要的一方面。今天在这里写出来，希望跟大家共勉。

此外是关于本文的结构，看上去每一篇的篇幅差别比较大。这一点主要是为了知识点的连贯性。比如第四篇，很多概念不连续介绍下来，恐怕在阅读源码阶段会碰到很多困难，只好放的比较长。在阅读的时候可以根据自己的情况做一些取舍及控制一下进度。

(待续…)

引文及参考

TensorFlow中文社区
Tensorflow 搭建自己的神经网络 (莫烦 Python 教程视频)
Overview of Artificial Neural Networks and its Applications
基于神经网络的激活函数和相应的数学介绍
An overview of gradient descent optimization algorithms