从锅炉工到AI专家(6)
TensorFlow实务
欠拟合和过拟合
几乎所有的复杂方程都存在结果跟预期差异的情况,越复杂的方程,这种情况就越严重。这里面通常都是算法造成的,当然也存在数据集的个体差异问题。
所以”欠拟合“和”过拟合“是机器学习过程中重要的调优指标之一。
如图所示:
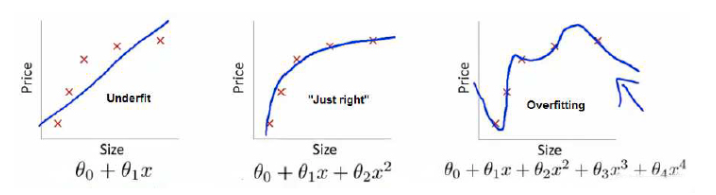
以篇(2)中房价的程序为例,上图中间的那幅图,是比较满意的一种结果。对于我们给出的所有样本,模型的预测结果同实际房价比较贴切的“拟合”。
左图则是“欠拟合”,有些样本和房价能对应的比较好,有些预测出来的值同事实则差距较大,“预测不大准”。
右侧图是“过拟合”,过拟合是很尴尬的一种情况,对于所有的训练样本都拟合非常好,但投产实际的数据就差别巨大。过拟合也很严重,在很多角度上比欠拟合更严重。如果在以前手工编写算法的年代,出现这种情况,模型的调优将会非常麻烦。并且在一个研发周期比较长的项目中,因为往往是到了投产阶段才发现过拟合问题,造成的损失也会比较大。
在分类问题中,一样会出现这两个问题,如图:

同样,中间的图表示拟合较好。左侧图表示欠拟合,右侧图表示过拟合。
欠拟合和过拟合情况发生之后,传统的办法有以下几种手段解决:
- 减少我们的参数数量,降低方程的维度。这个方法对于图像识别这种情况显然不适用,因为维度是固定的。
- 样本本身归一化做的不好。样本归一化我们前面说了,正常情况都应当先做归一化再进行训练。
- 通常增加样本的数量对改善“欠拟合”和“过拟合”都有效果。但是在工程中,样本就是钱啊。
- 手工实现的算法中,可以添加归一化参数(Regularization Parameter),通常称为λ。在TensorFlow这种成熟框架中,则使用了Dropout机制。
Dropout
Dropout可以当做神经网络中的一层,串联于神经网络中。接收上一层的输入,根据参数值抛弃一部分,把输出再接入到下一层输入,后面还是原来的神经网络。
这种方法对于整体算法几乎没有改变,代码变动最小,效果优秀。具体实现的数学公式在下面参考链接中有论文可供研究。TensorFlow中则已经有了内置的函数。
抛弃率也是一个学问,有论文表示,对于隐藏层来讲,50%的抛弃率有最优的效果,所以通常这部分就不用动脑子了,直接用0.5作为参数调用就好,不过我实际实践中,大多还是要尝试不同值看看效果。
最后同归一化参数λ的使用一样,在训练时,启用Dropout机制,也就是使用50%保留率(当然也是50%的抛弃率)调用tf.nn.dropout()。
等到实际生产的时候,因为模型用于真正预测,则无需再使用dropout。大多情况下我们训练的模型跟生产的模型,通常是同一个,这时候可以用100%保留率为参数调用dropout,等于所有数据都会输出,也就等于取消dropout层的效果。
注意,虽然函数名叫dropout,其中的参数确是表示数据保留下来的比例(当然不是简单的保留的意思,请参考后面的例子),其余的数据会用0替代。看一个小程序来验证dropout的效果:
#!/usr/bin/env python
# -*- coding=UTF-8 -*-
import tensorflow as tf
dropout = tf.placeholder(tf.float32)
x = tf.Variable(tf.ones([10, 10]))
y = tf.nn.dropout(x, dropout)
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
print sess.run(y, feed_dict = {dropout: 1})
print sess.run(y, feed_dict = {dropout: 0.1})
print sess.run(y, feed_dict = {dropout: 0.2})
上面例子分别使用参数1/0.1/0.2调用dropout,运行输出将是:
[[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]]
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 10. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[10. 0. 0. 0. 0. 10. 0. 0. 0. 0.]
[ 0. 0. 10. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 10. 0. 0. 0.]
[ 0. 10. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 10. 0. 0. 10. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0. 5. 0. 0. 0.]
[0. 0. 5. 5. 0. 0. 5. 5. 0. 5.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 5. 0.]
[0. 0. 5. 0. 5. 0. 0. 5. 5. 0.]
[0. 0. 0. 5. 0. 0. 0. 0. 0. 0.]
[5. 0. 0. 0. 0. 0. 0. 0. 0. 5.]
[0. 5. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 5. 0. 0. 0. 0. 5. 0.]
[5. 0. 0. 5. 0. 0. 0. 0. 0. 0.]]
dropout并不是简单的抛弃,每个保留下来的结果,实际上汇总了其它被设置为0的值。希望你对dropout彻底理解了。
卷积
通常讲,一项新技术的引入,往往是通常采用的技术发现了问题。为了解决这个问题经历大量研究和尝试之后,诞生了新的技术来对原有技术进行改进。卷积恰恰就是如此。
将DNN用于图像识别,识别率仍然不够高是表象。
一个很容易想到的根源则是一副二维的图片,变成了一维的浮点数组,其中点与相邻点之间的关系,本应当是这样图像识别中“图形”的部分理应关注的重点,而在DNN中反而完全把这种关系信息抛弃了。
为了改善这种情况,很早就曾经出现过名为“Edge filter”的算法,在神经网络的中间寻找这种可能出现的“边缘”的滤镜层,这其实就是卷积的雏形。
所采用的原理,你可以理解成用一副放大镜近距离、细致的观察一幅画面的局部,注意是二维的画面,不是一维的数组。
因为是局部,所以这个“卷积”核的维度不会很大,至少要远远小于整个要识别的图像。具体采用多大的尺寸,取决于你关注的那些边缘、或者笔画、或者微小的图形,是什么样的尺寸。在本案例中,将会采用5x5的卷积尺寸。
同时应当很容易理解,用放大镜观看图像嘛,看到的局部,虽然是一副小图像,但色深等特征,跟原图是一模一样的。所以卷积的深度,同原图必然是相同的,本例中是灰度图,1个数据的深度。如果是RGB彩色图,则是3个数据的深度。
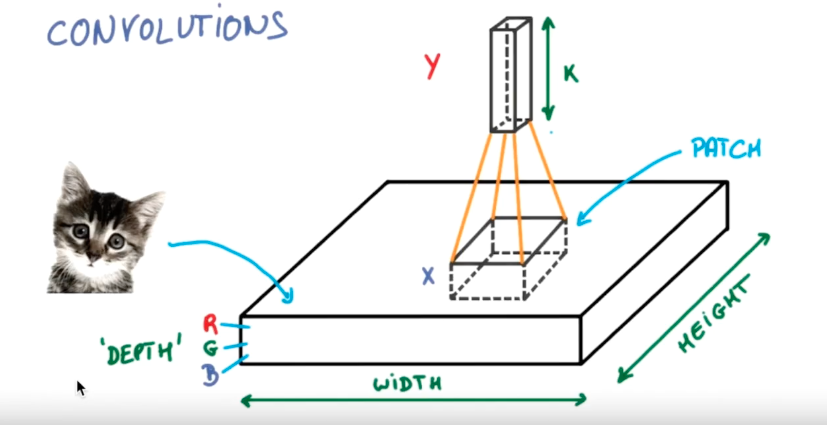
这个用于近距离、细致观察局部的小窗口,叫做“卷积核”,也有被称为“观察视野”的,同样都应当是转折的外来词,你理解含义,阅读文档的时候能看懂就好了。
“观察”这个小窗口所得到的信息,因为附加了边缘、笔画、图形等更精细的信息,这些信息显然不是原来的点阵图的概念。所以虽然这个窗口小了,但输出结果,必然要远远大于原有的深度。比如在本例中,我们使用5x5的窗口。而卷积输出的数据,原有图形仅是1维,这里将达到32维(这个值是我们根据本案例的需求,自行设置的)的深度。
这一点一定要注意,国内很多的译文中,不知道是哪个环节出的问题,居然很多人将卷积理解为“降维”的算法。这显然是没有真正理解卷积的内涵,并且把深度这么多倍的增长忽略掉了。
如同放大镜的边缘会稍有变形,卷积算法重点关注在卷积核中心,周围的数据也会有细微变形,这是由算法的数学模型决定的。
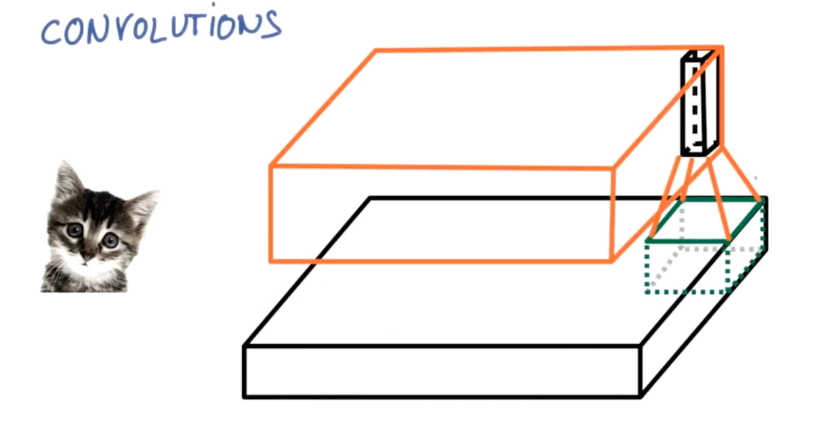
此外也如同放大镜在画面上一点点移动,逐渐观察整个画面一样,“观察窗”也将在屏幕上滚动,最终覆盖整个要识别的图像。这个滚动过程会有移动的步长设置,对于一些重点稀疏的图像,我们可能会增加步长来减少数据及提高效率。
因为上面这两个原因,卷积最终所得图像的输出尺寸,是可能小于原图像长宽尺寸的。这可能也是一部分人理解为降维的原因之一。但算上增加的深度,通常输出的数据,会几十倍于原有的输入数据量。
在本案例中,我们设置TensorFlow卷积的步长为1,padding参数为“SAME”,表示输出图像的尺寸跟原图完全相同。padding参数还可能取值为“VALID”,表示仅保留有效数据,这种情况下,即便步长仍然是1,因为刚才说过的边缘变形等原因,输出的尺寸也会缩小。
这里不断强调这一点,是因为多层神经网络之间,用于计算的矩阵维度,是互相对应的,你必须能清晰的知道你最终输入下一层的数据维度是什么。
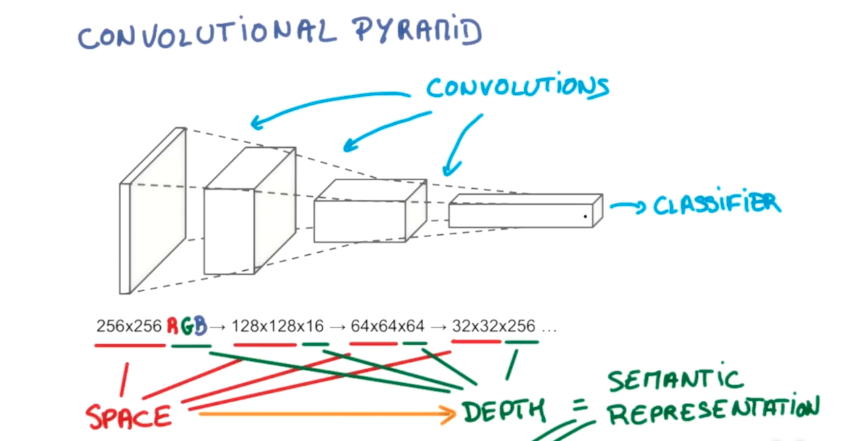
如同DNN一样,卷积也可以逐层关联,去深入挖掘信息与信息之间的细微关系。而卷积这种特点也逐层传递,成为尺寸越来越小,但深度越来越深的形状。用示意图来看,很像一个金字塔,所以也称为“卷积金字塔”。
问题来了,在我们这样的例子中,我们每一层都没有缩小图像尺寸,仅增加了深度。数据量逐层大幅增加,总会达到无法承受的境地啊?
而且,即便不考虑承受能力,假设我们所用的计算机无比强大,这些不是问题。但我们增加的数据,不可能凭空出现。从数学的推导来看,这些数据其实都是使用不同系数相乘而来的结果,原图中可能出现很小的一点误差,这样多倍的放大之后,必将也对结果产生很大的影响。这又如何解决呢?
池化
通常说,卷积跟池化都是联合使用的。
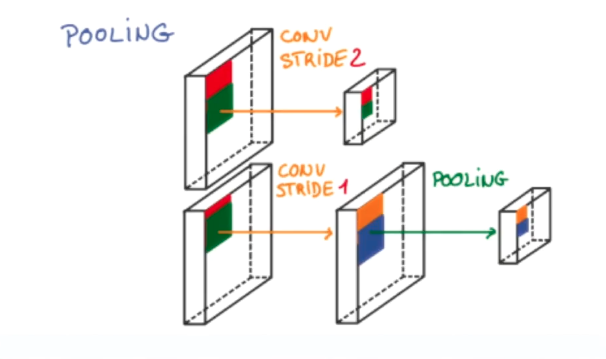
如图所示,上面部分,假设我们使用卷积的步长为2,那么会得到一个缩小一倍的数据量。
下面的部分,则是假设我们使用了步长为1,实际上得到的数据长宽尺寸,跟原图是相同的,而深度大大增加了。
这时候可以在卷积之后附加一层“池化”,以池化设置为2x2为例。池化算法会在输入的图像中,以2x2为视窗,提取其中的重点,形成一组数据。
在我们的案例中,等于输入2x2x32,输出1x1x32的数据。
在池化的“提取”中,有不同算法供选择,我们这里会采用max,就是取大者,这个大的部分不论在2x2的点阵中在哪一点,都会被提取出来。
所以池化算法对于消除数据抖动、增加系统鲁棒性也很有帮助。降维数据,则是本身就具有的能力。
TensorFlow中还提供了池化的“平均”提取算法,需要的时候可以查看TensorFlow相关资料。
总之在本例中,输入的图像经过2x2的池化之后,图像的深度不变,尺寸会长、宽各缩减一倍,数据总量将减少4倍。
网络模型构建
同DNN一样,CNN的构建也没有什么必须的规则。但是TensorFlow手写数字识别这个例子中所采用的构建方式被认为是比较典型的一种手段,在Google的教学视频中有介绍,相关的论文资料没有查到。
这里列出来供参考吧:
卷积层1->relu->池化层1->卷积层2->relu->池化层2->全连接神经网络层->relu->dropout层->神经网络输出层->softmax
总计11层,也算一个复杂的网络了。这个模式可以记下来,以后碰到新项目在自己还吃不准的时候,漫无目的大量实验之前套上这个模型试试,很可能会有惊喜的收获。
源码
提前说一下,每一次新的源码,其中跟以前例子重复的部分,我会减少注释或者取消注释,避免过多打断阅读程序的连贯性。
#!/usr/bin/env python
# -*- coding=UTF-8 -*-
import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
import tensorflow as tf
sess = tf.InteractiveSession()
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
#定义卷积,设定步长(stride size)为1,
#边距(padding size)为0,SAME就是指边距为0
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
#池化是2x2
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
x = tf.placeholder("float", shape=[None, 784])
y_ = tf.placeholder("float", shape=[None, 10])
#第一层卷积
#在每个5x5的patch中算出32个特征。卷积的权重张量形状是[5, 5, 1, 32],
#前两个维度是patch的大小,接着是输入的通道数目,这里灰度图是1个数据,
#最后是输出的通道数目。 而对于每一个输出通道都有一个对应的偏置量
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
#卷积是在平面2D图的方向上进行,
#所以为了使用这一层卷积,我们先要把x恢复成一组图,
#2D加上第一维是样本数量,以及图的色深,是一个4d向量,
#这里第2、第3维对应图片的宽、高,
#最后一维代表图片的颜色通道数(因为是灰度图所以这里的通道数为1,如果是rgb彩色图,则为3)。
x_image = tf.reshape(x, [-1,28,28,1])
#卷积计算,跟上个例子一样,使用relu激活函数
#本层卷积结果因为padding是SAME,
#所以输出同样是28x28,只是变成了32层深
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
#池化是2x2,所以输出结果是28/2=14,14x14x32的图
#max池化算法是指在2x2的空间中取最大值
h_pool1 = max_pool_2x2(h_conv1)
#第二层卷积:
#为了构建一个更深的网络,我们会把几个类似的层堆叠起来。
#第二层中,每个5x5的patch会得到64个特征。
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
#再次卷积,输出同输入一样是14x14,深度变成了64
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
#再次2x2池化,14/2=7,最后结果是7x7x64的图
h_pool2 = max_pool_2x2(h_conv2)
#密集连接层,也就是通常的神经网络层:
#现在,图片尺寸减小到7x7,接入到1024个神经元的全连接层
#因为传统神经网络层工作在一维模式,
#所以我们把池化层输出的张量reshape成一维向量
#算法跟上例中完全相同
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
#为了减少过拟合,我们在输出层之前加入dropout。
#我们用一个placeholder来代表一个神经元的输出在dropout中保持不变的概率。
#这样我们可以在训练过程中启用dropout,在测试过程中关闭dropout。
#TensorFlow的tf.nn.dropout操作除了可以屏蔽神经元的输出外,
#还会自动处理神经元输出的比例。
#所以用dropout的时候可以不用考虑比例。
#此外keep_prob更像是逻辑运算中的if then 逻辑,
#在机器学习中,利用规范的数学运算替代需要程序的逻辑运算是很常用的模式
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
#输出层:最后,我们添加一个softmax分类层
#对于这种分类型的深度学习,不管前面多么复杂的算法,
#最后往往仍然需要softmax进行分类
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
#训练和评估模型:
#请参考前一个源码中的注释
#在feed_dict中加入额外的参数keep_prob来控制dropout比例。然后每100次迭代输出一次日志。
cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
sess.run(tf.global_variables_initializer())
for i in range(20000):
batch = mnist.train.next_batch(50)
if i%100 == 0:
train_accuracy = accuracy.eval(feed_dict={
#测试过程同生产过程相同关闭dropout.
#1代表dropout的保留比例是100%,相当于没起作用
x:batch[0], y_: batch[1], keep_prob: 1.0})
print "step %d, training accuracy %g"%(i, train_accuracy)
#训练过程,启用dropout,保留50%
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
print "test accuracy %g"%accuracy.eval(feed_dict={
x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0})
这个真的是当前比较先进的识别算法了,最终的正确率大约是超过98%,绝对达到了商用的标准。只是在运行的时候你可能注意到了,三个不同的实现,模型训练的速度一个比一个慢。为了提高这2%的识别率,可说无比艰辛。
从视觉上看卷积的本质
我们说过了卷积在这里主要用于提取细节中相邻点之间的关系。这里“视觉”就是指肉眼能看到的线、边、笔画、小图形。
那么如果把这些卷积的结果图形化出来是什么样子呢?下图就是一个展示:
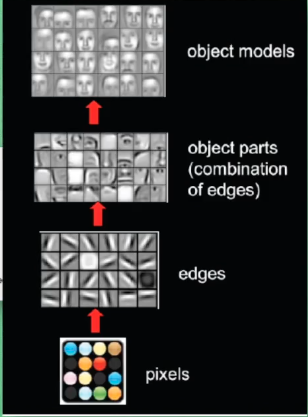
是不是看到这种直观的图示令人更印象更深刻?
所以由于这些特点,CNN大量的用于图像识别、人脸识别、文字识别、语音识别等很广泛的领域,涵盖当前比较火爆的机器学习中很大一部分行业。到了这里,你也可以自豪的喊一声:真的入行了。
(待续…)
